FREE INDUCTION DECAY: An MLAB Example
Introduction
Consider the following experiment: a 1 cubic centimeter sample of water at room
temperature is placed between the pole faces of a 10,000 Gauss (1 Tesla)
electromagnet. As the system reaches equilibrium, a small magnetic dipole of
magnitude 3.4E-6 Gauss is induced in the sample parallel to the applied field.
Designate the axis passing from the south pole to the north pole of the magnet
as the z-axis with the origin at the center of the sample, midway between the
magnet's pole faces. The sample is surrounded by two thin wire coils such that
the axes of the coils are perpendicular to each other and to the z-axis. The
axes passing through the center of the coils are designated the x and y axes. A
brief 42 megahertz alternating current pulse is applied to the x-axis coil. If
the pulse is of the appropriate amplitude and duration, it causes the induced
magnetic dipole to tilt away from the z-axis. The magnetic dipole then precesses
around the z-axis, gradually returning to its equilibrium position parallel to
the z-axis. The component of the magnetic dipole which rotates in the xy-plane
induces 42 megahertz oscillating voltages-90 degrees out of phase-across the
terminals of the two coils which die away in time.
These signals are termed free induction decay signals and they are the
basic physical effect which underlies modern day magnetic resonance imaging (MRI)
and nuclear magnetic resonance (NMR) experiments. Free induction decay can be
described by a model developed by F. Bloch in the paper ``Nuclear Induction''
Phys. Rev. 70 (1946) 460. The mathematical formulation of the model is called Bloch's
equations and consists of 3 ordinary differential equations:
|
(0.1) |
|
(0.2) |
|
(0.3) |
This paper will demonstrate how the MLAB mathematical modeling system can be used to solve Bloch's equations to predict free induction decay signals in single and double pulse experiments. MLAB is a computer program whose name is an acronym for ``Modeling LABoratory''. It is an interactive interpreter like Basic but with sophisticated instructions for solving ordinary differential equations, curve fitting, and generating publication quality graphs. It was originally developed at the National Institutes of Health. It is available from Civilized Software for most current computer platforms.
A Single [(p)/4] Pulse Experiment
To begin using MLAB, double click on the MLAB icon-if running an operating
system with a graphical user interface, or type mlab at the operating
system prompt for DOS or Unix systems. MLAB then types some initialization
information on the screen and an asterisk, *. The asterisk is the
prompt for the user to type MLAB instructions. In what follows, MLAB
instructions will be typed in bold face on lines beginning with *
and comments will be delimited by /* and */. Although it is
not shown, the < Enter > key should be struck at the end of each line.
We begin by simulating a single pulse experiment which rotates the magnetic dipole of the sample by p/4 radians about the x-axis. First define Block's equations by typing:
* function mx't(t) = g*(my*hz(t)-mz*hy(t))-mx/t2 * function my't(t) = g*(mz*hx(t)-mx*hz(t))-my/t2 * function mz't(t) = g*(mx*hy(t)-my*hx(t))+(m0-mz)/t1
The function statement allows the user to define any algebraic or differential equation model desired. The apostrophe, ', denotes the differentiation operation.
Next assign values to the constants appearing in the function statements by typing
* g = 2.66E4 /* gyromagnetic ratio for protons */ * m0 = 3.4E-6 /* equilibrium magnitude of magnetic dipole in Gauss */ * t1 = 1.E-6 /* spin-lattice relaxation time in seconds */ * t2 = 1.E-6 /* spin-spin relaxation time in seconds */ * beta1 = pi/4 /* rotation angle for first pulse in radians */ * h0 = 10000 /* magnitude of external magnetic field in Gauss */ * fct hx(t) = 0 /* x-component of external magnetic field in Gauss */ * fct hy(t) = 0 /* y-component of external magnetic field in Gauss */ * fct hz(t) = h0/* z-component of external magnetic field in Gauss */
The magnetic field is defined as having only a z-component of 10000 Gauss. For a normal water sample, T1 is roughly 1 second and T2 is roughly 1 millisecond. Fictitious values for the spin-lattice and spin-spin relaxation constants have been selected here so that the effect of relaxation can be observed in the time scale of several precessions of the induced magnetic dipole.
The magnetic dipole vector will precess about the z-axis at the Larmor frequency, w = [(gH0)/(2p)] = 42 megahertz. We will solve Bloch's equations for ten precessions sampled at 300 time points. Define a vector t with components equal to the times of observation.
* nsteps = 300 * tau = 10*2*pi/(g*h0) * t = 0:tau!nsteps
The -:-!- construct in the last statement instructs MLAB to make t a row vector with components 0 to tau in 300 steps. We can now simulate the single pulse experiment by defining a so-called macro which initializes the components of the magnetic dipole vector at time 0 after the pulse and then integrates the differential equation model.
* pulse1 = "initial mx(0) = 0;
initial my(0) = sin(beta1)*m0;
initial mz(0) = cos(beta1)*m0;
m = points(mx,my,mz,t);"
Here the initial statements provide the initial conditions for the differential equations-the equilibrium dipole moment is rotated by an angle beta1 about the x-axis. The points operator solves the differential equations for mx, my, and mz at the times listed in t. The points operator returns a 4 column array with time in column 1, and the x, y, and z components of the magnetic dipole vector in columns 2, 3, and 4, respectively. The macro is executed as follows:
* do pulse1
We can generate a 3 dimensional perspective figure of the time evolution of the magnetic dipole vector by defining another macro:
* mdip = "delete m col 1;
m = (0^^'3) m;
draw m lt sequence;"
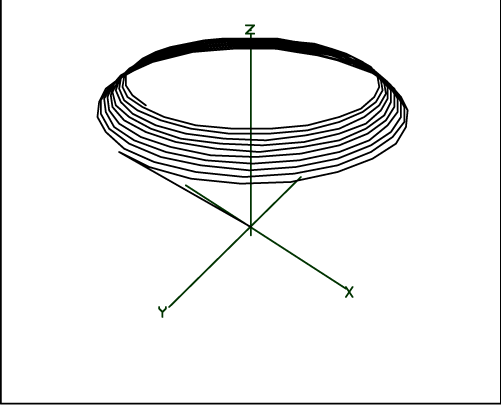
This macro instructs MLAB to throw away the time information in column 1 of the matrix m, add the origin (0,0,0) to the list of magnetic dipole vector components, and draw the resulting sequence of points. We execute the macro with some 3 dimensional perspective positioning commands as follows:
* do mdip
* cmd3d("raise 1") /* raises the point of view */
* cmd3d("truck 1") /* moves the point of view to the right */
* cmd3d("track") /* points the direction of view to the center */
* cmd3d("dolly 1") /* moves the point of view toward the subject */
* cmd3d("twist -20") * cmd3d(äxes") /* draws coordinate axes */
* view
The following picture then appears on the display:

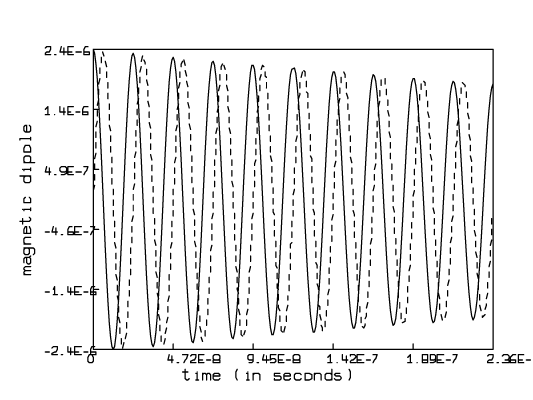
The transverse component of the magnetic dipole can be decomposed into x and y components. It is the variations of the components of the magnetic dipole along the x and y axes which give rise to the free induction decay signals. These can be drawn by defining and executing another macro.
* unview /* remove the 3d picture */
* delete w3
* btitle = "time (in seconds)"
* ltitle = "magnetic dipole"
* emfs = "delete m row 1;
draw t ' m col 1 lt dashed;
draw t ' m col 2;
bottom title btitle;
left title ltitle;"
* do emfs
* view
The macro emfs draws a graph of the x-component of the magnetic dipole versus time with a dashed line and the y-component of the magnetic dipole versus time with a solid line. It also places titles on the bottom and left axes.
The following picture is then seen on the display:
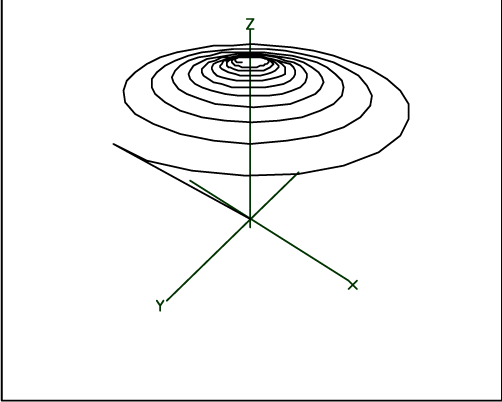
With the macros pulse1, mdip, and emfs defined above, it is a simple matter to change the relaxation constants, the pulse's angle of rotation, the strength and direction of the external magnetic field, or the gyromagnetic ratio and run the single pulse experiment again. For example, suppose the spin-spin relaxation constant, T2, is smaller by a factor of 10. The following commands generate the 3 dimensional perspective picture and the 2 dimensional time plot of the components of the magnetic dipole vector:
* unview /* remove the previous picture */
* delete w
* t2 = 1.E-7 /* re-define the spin-spin relaxation constant */
* do pulse1 /* run the experiment */
* do mdip /* draw the 3d picture */
* cmd3d("raise 1")
* cmd3d("truck 1")
* cmd3d("track")
* cmd3d("dolly 1")
* cmd3d("twist -20")
* cmd3d("axes")
* view
* unview /* remove the previous picture */ * delete w3 * do emfs /* draw the time-dependent magnetic dipole components */ * view
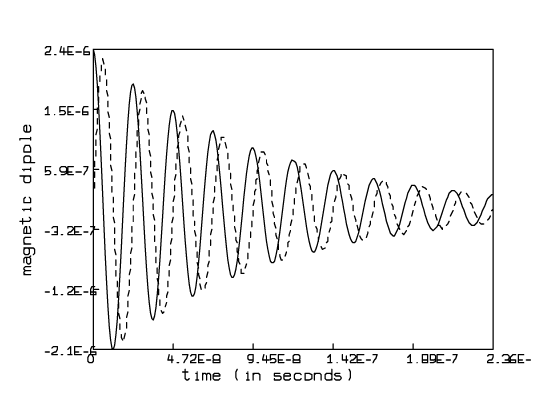
* unview /* remove the previous picture */ * delete w
As expected, the smaller value of the spin-spin relaxation time, T2 causes the free induction decay signal to die away faster than in the previous example.
A Double Pulse Experiment
If the external magnetic field is not homogeneous, double pulse
experiments can be performed which give rise to resurgences of amplitude in the
free induction decay signals. This effect was described by E.L. Hahn in the
article ``Spin Echoes'' Phys. Rev. 80 (1950) 580. Here we simulate a double
pulse experiment consisting of a pulse sequence in which the first pulse rotates
the magnetic dipole by [(p)/2] radians about the
x-axis and the second pulse-t units of time
later-rotates the magnetic dipole by p radians about
the x-axis. Owing to the inhomogeneities in the external magnetic field, the
resurgence of amplitude in the free induction decay signal is observed t
units of time after the second pulse.
The inhomogeneity of the external magnetic field is simulated by running the pulse sequence on 10 magnetic dipoles, each subject to a different constant, external magnetic field. The Larmor frequency of precession is different for each magnetic dipole. The spin echo is then observed in the net magnetic dipole obtained by summing the time dependent free induction decay signals from each of the magnetic dipoles.
First we show the free induction decay resulting from the pulse sequence applied to a magnetic dipole in a homogeneous magnetic field. The macro pulse1 from the previous section can be used to generate the time evolution of the magnetic dipole from the moment of the first pulse to the moment before the second pulse. We define a vector of times tt which holds times for the rest of the experiment.
* tt = tau:(2.5*tau)!(1.5*nsteps)
This statement assigns tt the values tau to 2.5*tau in 450 steps. Then we define a new macro, pulse2, which determines the effect of the second pulse.
* pulse2 = "initial mx(tau) = m[nsteps,2];
initial my(tau) = m[nsteps,3]*cos(beta2)+m[nsteps,4]*sin(beta2);
initial mz(tau) = -m[nsteps,3]*sin(beta2)+m[nsteps,4]*cos(beta2);
m = m points(mx,my,mz,tt);"
The initial statements in this macro find the components of the magnetic dipole at time tau after the second pulse has rotated the magnetic dipole about the x axis by an angle beta2. The points operator in the fourth statement solves Bloch's equations for the times in the vector tt and the ampersand operator concatenates the four column solution matrix from the points operator to the existing matrix m where the time evolution of the magnetic dipole from 0 to tau has been stored.
The following MLAB commands perform the complete double pulse sequence on a magnetic dipole in a 10000 Gauss homogeneous magnetic field:
* beta1 = pi/2 * beta2 = pi * t2 = 5.E-7 * do pulse1 * do pulse2
To see the time evolution of the magnetic dipole in a 3 dimensional perspective, type:
* do mdip
* cmd3d("raise 1")
* cmd3d("truck 1")
* cmd3d("track")
* cmd3d("dolly 1")
* cmd3d("twist -20")
* cmd3d("axes")
* view
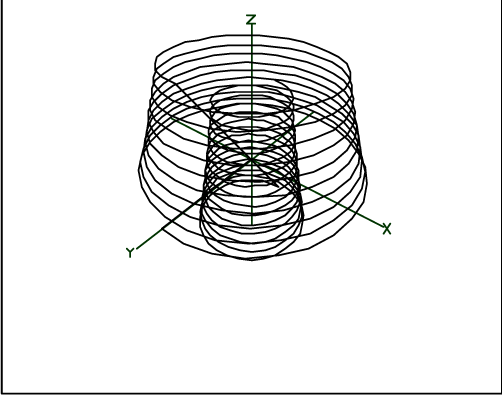
The x and y components of the magnetic dipole, which are proportional to the free induction decay signals, are shown by the commands
* unview * delete w3 * ttt = t * t = t & tt * do emfs * view
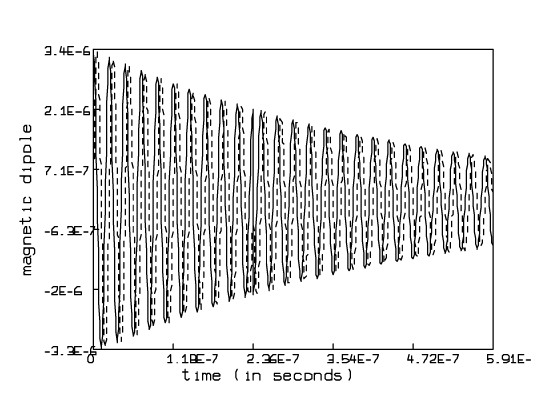
* unview * delete w * t = ttt
To demonstrate the spin echo effect, we determine the time evolution of the average of 10 distinct magnetic dipoles-each evolving in a different magnetic field. This is accomplished with the following commands:
* h00 = 9600:10400!10 /* the different magnetic fields */
* netp = shape(750,3,0^^2250);
* for i = 1:10 do {
> h0 = h00[i]
> do pulse1
> do pulse2
> delete m col 1
> netp = netp+m
> }
First we set h00 to be a vector of magnetic field strengths ranging in value from 9600 Gauss to 10400 Gauss in 10 steps. Actual inhomogeneities in the external magnetic field are on the order of .01 Gauss. Here, the inhomogeneity in the 10000 Gauss external magnetic field is greatly exaggerated so that the spin echo effect can be demonstrated in a short time interval.
The shape operator is then used to initialize the 750 row by 3 column matrix netp to zero. The for...do loop runs the double pulse experiment ten times. Each time, the magnetic field is different and the time evolution of the magnetic dipole computed in m is accumulated in the array netp.
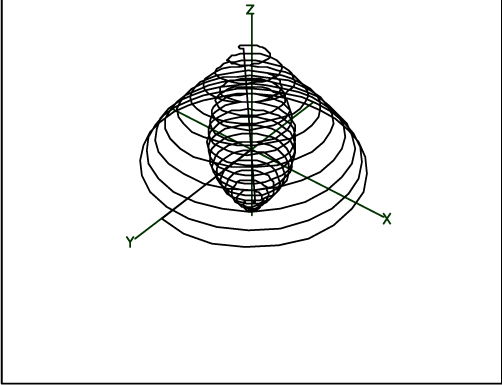
The 3 dimensional perspective view of the evolution of the net magnetic dipole is shown by the following commands:
* netp = (0^^'3) netp
* draw netp lt sequence * cmd3d("raise 1")
* cmd3d("truck 1")
* cmd3d("track")
* cmd3d("dolly 1")
* cmd3d("twist -20")
* cmd3d("axes")
* view
* unview * delete w3 * delete netp row 1 * draw (t & tt) &' netp col 1 lt dashed * draw (t & tt) &' netp col 2 * bottom title btitle * left title ltitle * view
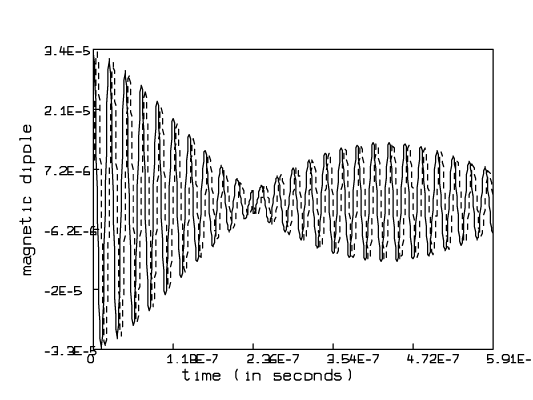
* unview * delete w Conclusion
This paper has demonstrated how MLAB can be used to explore a specific
differential equation model: Bloch's equations for a magnetic dipole in an
external magnetic field. MLAB contains a large collection of functions,
including Fourier transforms, non-linear optimization, curve fitting,
statistical distribution functions and their inverses, and orthogonal
polynomials.