Contour Maps

MLAB has a very powerful contour map algorithm. It computes a matrix holding the points on the individual level curves, so that their paths can be used in further computations, as well as graphed when desired. (Many contour algorithms produce plots, but do not produce explicit numbers, so nothing can be done with such algorithms, except look at the produced plot.) The paths generated with the MLAB CONTOUR operator are guaranteed to be non-self-intersecting. The most complex pattern that can arise is a four-leaf-clover shape.

The MLAB CONTOUR operator does require that the data points of the surface to be ``contoured'' are given corresponding to a regular grid. If only irregularly-positioned points are known, the surface interpolation function can be used to obtain data points on a regular grid by nearest-neighbor average triangle interpolation.

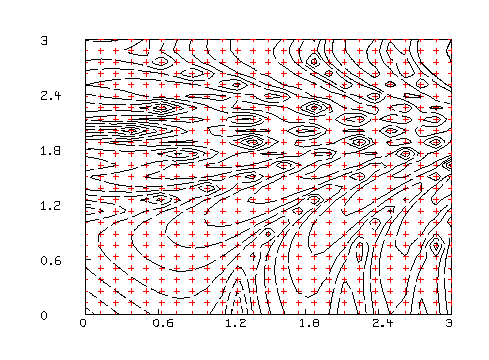
Some examples of contour maps produced in MLAB are given below.

Example 1:

Plot a contour map of the function

f(x,y) = sqrt(abs(cos(x

²-y³))) + log(abs(x+y)+1)
in the rectangle

[0,3]

^. [0,3].

contour map for the function $f(x,y) = sqrt(abs(cos(x$ ²-y³))) + log(abs(x+y)+1) in $[0,3]$ ^. [0,3].

The MLAB commands to do this are given below.

* FUNCTION F(x,y) = SQRT(ABS(COS(X^2-Y^3))) + LOG(1+ABS(X+Y))
* M = CROSS(0:3!25, 0:3!25)
* M COL 3 = F ON M
* DRAW CONTOUR(M) LINETYPE SVMARKER
* DRAW M COL 1:2, LINETYPE NONE, POINTTYPE CROSSPT, PTSIZE .01 COLOR YELLOW
* VIEW

We can also look at our surface using the MLAB $3D$ graphics facilities as follows.

* DELETE W
* DRAW M LINETYPE HIDDEN
* VIEW

3D picture corresponding to the previous contour map

Example 2:

Plot a contour map of the

441

data values stored in the file CDATA.DAT which are the elevations of a surface, stored by rows, corresponding to the grid

{0,1,...,20}

^. {0,1,...,20}.

* D = READ(CDATA,21,21)
* D = CROSS(0:20,0:20) &' LIST(D)
* C = CONTOUR(D,30)
* DRAW C LINETYPE SVMARKER
* DRAW D COL 1:2, LT NONE, PT CROSSPT, PTSIZE .01, COLOR YELLOW
* VIEW

contour map for the surface described by the data points in CDATA.DAT.

We can also look at our surface using the MLAB $3D$ graphics facilities as follows.

* DELETE W
* DRAW M LINETYPE HIDDEN
* VIEW

3D picture corresponds to the previous contour map

Note we have not described how hard-copy plots are made, but this document shows plotting can be easily done.