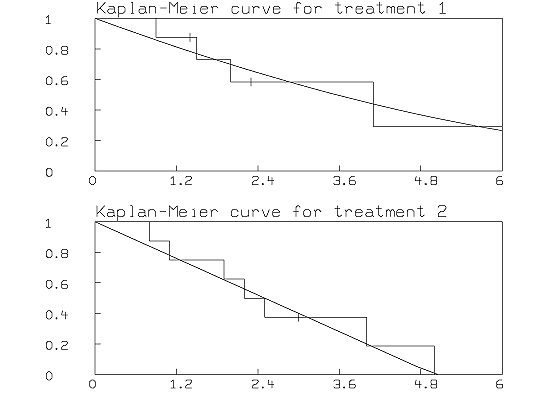
Maximum Likelihood Survival Curve Estimation



Let X1, ¼, Xk be independent positive random variables representing the survival times of k subjects. Each subject has an associated set of n covariate values which serve to categorize that subject. Let xi = (xi1, ¼, xin) be the vector of covariate values for subject i. The distribution of the survival time Xi is postulated to depend on the covariate values for subject i.

Let F(t;x) = P[a subject with covariate values x = (x1, ¼, xn) has a failure time £ t]. The function F maps Rn+1 to R.

The associated density function is f (t; x) : = dF(t; x)/dt, and the associated survival function is S(t; x) : = 1 - F(t; x). The associated hazard function is h(t; x) : = f(t; x) / S(t;x). Note that log (h(t; x)) = log(f(t; x)) - log( S(t; x)).

Let C1, ¼, Ck be independent identically distributed positive random variables. Ci represents the length of time beyond which subject i is not observed. If Ci < Xi then subject i is lost to follow-up, that is the survival time of subject i is unknown; we know only that subject i survived at least Ci years. Let Yi = min(Xi, Ci), and suppose we observe values (i.e. samples) y1, ¼, yn of Y1, ¼, Yk. When Ci < Xi, we say that the value yi is a censored observation. We will define the indicator code zi = 0 when yi is a censored observation and otherwise zi will be defined to be 1.

Now suppose we are given the data:
subject#
covariates
time
censor-code
1
x11, ¼, x1n
y1
z1
:
:
:
:
k
xk1, ¼, xkn
yk
zk

Thus subject j with the covariate values xj1, ¼, xjn has the time to failure equal to yj when zj = 1, or alternately was lost to follow-up after time yj when zj = 0. Given this data, our goal is to construct a descriptive model, i.e. an estimate, for the underlying distribution function F.

We may form the likelihood function for this data as follows:


L =
Õ
{ i | zi = 1 }
f(yi; xi) ×
Õ
{ i |zi = 0 }
S(yi; xi)

The corresponding log-likelihood function can be seen to be


G = k
å
i = 1 
 log(S(yi; xi)) + zi · log(h(yi; xi)).

Now suppose that F depends upon some parameters a = (a1, a2, ¼,an) and b = (b1, b2, ¼, bn). Then f, S and h also depend on the vectors a and b, and the log-likelihood function G is a function of a and b alone. Thus


G(a, b) = k
å
i = 1 
 log(S(yi; xi; a, b)) + zi · log(h(yi;xi; a, b)).

If we postulate a specific form for F (and hence for S, f, h and G), we can estimate the parameters a1, a2, ¼,an and b1, b2, ¼, bn by choosing a and b to maximize G(a,b). This provides a potentially-enlightening descriptive model for our given data.

 

Piantadosi has proposed the model


h(t; x; a, b) =  b(x,b)
a(x,a) + S(t; x; a, b)

where


a(x, a) = exp ( a1 x1 + ¼+ an xn)

b(x, a) = exp ( b1 x1 + ¼+ bn xn).

This model defines F implicitly. In particular S satisfies the differential equation


 dS
dt
 (t; x; a, b) =  - b(x, b) S(t; x; a,b)
a(x,a) + S(t; x; a, b)
with S(0;x;a,b) = 1.

Since S(t;x;a,b) ·h(t;x;a,b) = dF(t;x;a,b)/dt, this differential equation corresponds to the algebraic relationship:


a(x,a) log (S(t;x;a,b)) + S(t;x;a,b) = 1 - b(x,b) t,

and since a(x,a) > 0, b(x,b) > 0, t ³ 0, and S(0;x;a,b) = 1, there is always a solution for S(t;x;a,b) in [0,1].

Now our log-likelihood function becomes:


G(a,b) = k
å
i=1 
 log(S(yi;xi;a,b)) + zi [log(b(xi,b)) -log(a(xi,a) + S(yi;xi;a,b))].

In order to estimate a and b for this model via maximizing the log-likelihood, we may use the maximize functional in MLAB. An example of this for n = 3, where the parameters become a1, a2, a3,b1, b2, b3, is given below for the following data. Here x1 is fixed equal to 1 for all subjects in order to introduce constant terms in log(a(x,a)) and log(b(x,b)); and xi2 = 1 when subject i had treatment 1 and xi3 = 1 when subject i had treatment 2. The observed survival time for subject i was truncated (censored) if zi = 0.


subject#
x1
x2
x3
y
z
1
1
1
0
2.3
0
2
1
0
1
4
1
3
1
0
1
5
1
4
1
0
1
2.2
1
5
1
1
0
6
0
6
1
0
0
3.6
1
7
1
1
0
4.1
1
8
1
1
0
2
1
9
1
1
0
1.5
1
10
1
0
1
3
0
11
1
0
1
2.5
1
12
1
0
1
0.8
1
13
1
1
0
0.9
1
14
1
0
1
1.1
1
15
1
1
0
1.4
0
16
1
0
1
1.9
1
17
1
1
0
2.3
0

Here is the MLAB dialog that uses the survival model in Piantadosi and Crowley, Biometrics (in press). 

"log-likelihood function"
fct g() = sum(i,1,k,gt(alpha(i),betav(i), i))
fct gt(av,bv,i) = gs(logs(av,bv*t[i]/av), z[i],av,bv)
fct gs(ls,z,av,bv) = ls + z * (log(bv) - log(av+exp(ls)))
fct logs(av,ub) = root(w,0,ub,av*w+exp(w-ub)-1)-ub
fct alpha(i) = exp(a1*x[i,1]+a2*x[i,2]+a3*x[i,3])
fct betav(i) = exp(b1*x[i,1]+b2*x[i,2]+b3*x[i,3])

/* surv1, surv2 = survival function for treatment 1 and treatment 2 groups */
fct av1(s) = max(1e-30,exp(a1 + s*a2 + (1-s)*a3))
fct bv1(s) = max(1e-30,exp(b1 + s*b2 + (1-s)*b3))
fct surv(t,s) = exp(logs(av1(s),bv1(s)*t/av1(s)))
fct surv1(t) = surv(t,1);
fct surv2(t) = surv(t,0);

n = 3; "# of covariates "
k = 17; ßample size"

data = read(datafile,k,n+2)

x = data col 1:n
t = data col (n+1)
z = data col (n+2)

/* establish initial guesses */
a1 = 0; a2 = 0; a3 = 0; b1 = -2; b2 = -2; b3 = -2;

Hessmsw = 0; /* starting with identity Hessian */
maximize(g,b3,b2,b1,a3,a2,a1)

The function value is: -2.389855e+01
Argument(s): (-3.284358e-01 -7.916285e-02 -1.281012e+00 
              -2.723759e+00 1.824017e+01 -1.877267e+01 )
Gradient: (3.302230e-01 4.906215e-03 1.718221e-01 
          -4.880071e-05 -1.584679e-03 -1.723857e-03 )
# of function evaluations: 242
# of gradient evaluations: 99
# of Quasi-Newton iterations: 94
    = -23.8985504

We will use the MLAB function KMSURV to compute and plot the two Kaplan-Meier survival curves and compare them with the estimated survival curves for treatment 1 and treatment 2. 

/* draw the Kaplan-Meier curve and surv1 for treatment 1 in w1. */
d1 = compress(data,2); /* data for first treatment */
d = (d1 col 4) &' (d1 col 5)

d = sort(sort(d,2,-1),1)
"double sorting makes censored events occur in front of failure events if 
 they happen at the same time."
h1 = kmsurv(d); "Column (1,2) of h1 is the Kaplan-Meier survival curve for d"

h = stepgraph(h1 col (1,2))
r = (0 &' 1) & h & (h[nrows(h),1] &' 0); "the graph starts at (0,1)"
draw r, color red; "Draw the step-graph of the Kaplan-Meier curve"

"draw censored data tic-marks"
y1 = compress(d,2,1) col 1; ÿ1 = the list of censoring times"
fct f(x) = lookup(h,x)

draw points(f, y1) lt none, pt vbar, ptsize .015, color green
top title "Kaplan-Meier curve for treatment 1"
frame 0 to 1, .5 to 1
"draw the estimated survival curve for treatment 1"
draw points(surv1,0:6!20)
w1 = w

/* draw the Kaplan-Meier curve for treatment 2 in w2. */
d2 = compress(data,3); /* data for second treatment */
d = (d2 col 4) &' (d2 col 5)

d = sort(sort(d,2,-1),1)
h1 = kmsurv(d); "Column (1,2) of h1 is the Kaplan-Meier survival curve for d"

h = stepgraph(h1 col (1,2))
r = (0 &' 1) & h & (h[nrows(h),1] &' 0); "the graph starts at (0,1)"
draw r, color red; "Draw the step-graph of the Kaplan-Meier curve"

"draw censored data tic-marks"
y1 = compress(d,2,1) col 1; ÿ1 = the list of censoring times"
fct f(x) = lookup(h,x)

draw points(f, y1), lt none, pt vbar, ptsize .015, color green
top title "Kaplan-Meier curve for treatment 2"
frame 0 to 1, 0 to .5
draw points(surv2,0:6!20)
w2 = w
view

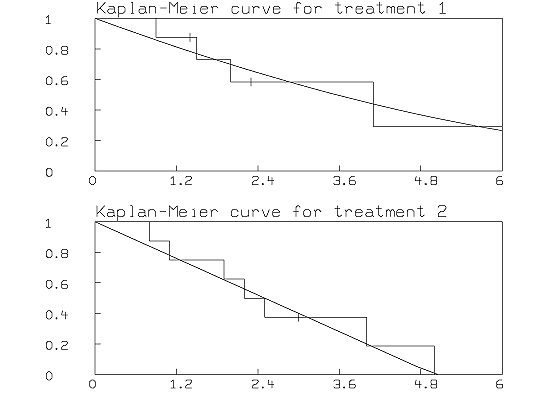
Here is the entire surface plot for the function surv. 

M = cross(0:6!17, 0:1!13)
M col 3 = surv on M
del w1, w2
draw M lt hidden
view