![[Previous Document]](http:/Images/Left.gif)
![[Back to CSI Home Page]](http:/Images/Home.gif)
![[Next Document]](http:/Images/Right.gif)
Here is an example which shows off each of the above features. Can you spot where each feature is exhibited?
fct g't(t) = a*g(t-d) + h*root(z,-b,b, acos(z/b)-1/(t+1))
fct h't(t)=cos(t-a)*g
initial g(0)=c
initial h(0)=1
a=.1; b=1; c=.5; d=.1;
m1= read(gdata,100,2)
m2= read(gddata,100,2)
fct wg(m,j)=abs(m[j,2]-sqrt(g))
constraints q={a>0, b>1, .1<c, c<1}
wr=ewt(m2)
fitnorm=1
fit(a,b,c,d),g to m1 with weight wg, g't to m2 with weight wr, constraints q
final parameter values
value error dependency parameter
8.326672685e-17 0.3825860609 0.983098032 A
1.009375311 0.8904044698 0.9920220641 B
1 7.341169978 0.9966718057 C
0.5318706953 1.797693135e+308 1 D
2 iterations
CONVERGED
best weighted sum of squares = 9.072228e+04
weighted root mean square error = 5.593169e+01
weighted deviation fraction = 8.740915e-01
lagrange multiplier[1] = -8986.559879
lagrange multiplier[4] = 250.7190973
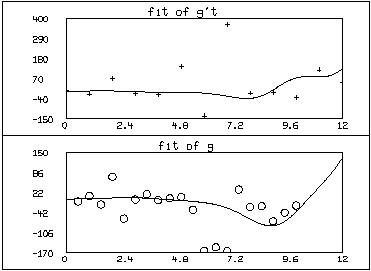
draw m1 pt circle lt none
draw points(g,0:12!160) color red
top title "fit of g"
frame 0 to 1, 0 to .5
w1=w
draw m2 pt "+" lt none
draw points(g't,0:12!160) color green
top title "fit of g''t"
frame 0 to 1, .5 to 1
view
![[Previous Document]](http:/Images/Left.gif)
![[Back to CSI Home Page]](http:/Images/Home.gif)
![[Next Document]](http:/Images/Right.gif)